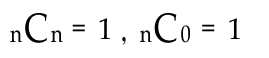Jenikeju

내가 푼 풀이

- 이 문제는 배낭문제로 유명하다. Knapsack

- 최적의 원리를 만족하게끔 점화식을 낸다.

- 최적의 원리: 어떤 문제의 입력사례의 최적해가 그 입력사례를 분할한 부분사례에 대한 최적해를 항상 포함하고 있으면, 그 문제에 대하여 최적의 원리가 성립한다.

- i개의 물건이 있을때,

• i번째 물건을 가져가지 않을때: i-1개의 물건들 중에서 최적의 가치의 값과 같다.
• i번째 물건을 가져갈때:  i-1개의 물건들 중에서 최적의 가치를 지니며, i번째 물건의 가치를 더한것과 같다.

- dp[i][j] : i개의 물건과 j의 무게한도를 가질때, 최고의 가치를 의미한다면

• i번째 물건이 배낭에 넣을 수 없을때: i-1개가 들어간 배낭이 최적의 가치를 가져야한다. (i-1단계의 값을 불러온다.)
• i번째 물건을 넣을 수 있을때: i번째 물건의 무게를 비울때의 최적값에 i번째 물건의 가치를 더한값 혹은 i-1개의 물건의 가치중 큰 수를 넣는다.

import Foundation

let input = readLine()!.split(separator: " ").map{ Int(String($0))! }
var dp = Array(repeating: Array(repeating: 0, count: input[1]+1), count: input[0]+1)
var weight = Array(repeating: 0, count: input[0] + 1)
var value = Array(repeating: 0, count: input[0] + 1)

for i in 1...input[0] {     // 해당 물건의 무게와 가치를 저장
    let item = readLine()!.split(separator: " ").map{ Int(String($0))! }
    weight[i] = item[0]
    value[i] = item[1]
}

for i in 1...input[0] {         // i는 물건의 갯수, 접근은 i번째 물건
    for j in 1...input[1] {     // j는 무게
        if weight[i] <= j {     // i번째 물건이 j만큼의 무게한도 배낭에 들어갈 수 있는 경우
            dp[i][j] = max(dp[i-1][j-weight[i]] + value[i], dp[i-1][j])
            // -> i번째 물건을 넣기위해 해당 무게를 비웠을 때의 최적값에 i번째 물건의 가치를 더한 값과
            // -> i번째 물건을 넣지않은 이전 최적값 중 큰값을 선택한다.
        } else {
            dp[i][j] = dp[i-1][j]   // i번째 물건을 넣을 수 없다면 i-1의 최적값을 선택
        }
    }
}

print(dp[input[0]][input[1]])   // N개의 물건과 W의 무게한도가 주어진 배낭의 최적값 출력

knapsack 출처:

문제

상담원으로 일하고 있는 백준이는 퇴사를 하려고 한다.

오늘부터 N+1일째 되는 날 퇴사를 하기 위해서, 남은 N일 동안 최대한 많은 상담을 하려고 한다.

백준이는 비서에게 최대한 많은 상담을 잡으라고 부탁을 했고, 비서는 하루에 하나씩 서로 다른 사람의 상담을 잡아놓았다.

각각의 상담은 상담을 완료하는데 걸리는 기간 Ti와 상담을 했을 때 받을 수 있는 금액 Pi로 이루어져 있다.

N = 7인 경우에 다음과 같은 상담 일정표를 보자.

1일에 잡혀있는 상담은 총 3일이 걸리며, 상담했을 때 받을 수 있는 금액은 10이다. 5일에 잡혀있는 상담은 총 2일이 걸리며, 받을 수 있는 금액은 15이다.

상담을 하는데 필요한 기간은 1일보다 클 수 있기 때문에, 모든 상담을 할 수는 없다. 예를 들어서 1일에 상담을 하게 되면, 2일, 3일에 있는 상담은 할 수 없게 된다. 2일에 있는 상담을 하게 되면, 3, 4, 5, 6일에 잡혀있는 상담은 할 수 없다.

또한, N+1일째에는 회사에 없기 때문에, 6, 7일에 있는 상담을 할 수 없다.

퇴사 전에 할 수 있는 상담의 최대 이익은 1일, 4일, 5일에 있는 상담을 하는 것이며, 이때의 이익은 10+20+15=45이다.

상담을 적절히 했을 때, 백준이가 얻을 수 있는 최대 수익을 구하는 프로그램을 작성하시오.

내가 푼 풀이

- dp[n] 은 n일째 받을 수 있는 최대 수익

- n을 정순으로 가면 dp[n+i] = max(dp[n] + pay, dp[n+i]) 로 최대 수익을 최신화 해도되지만, n번째에 상담을 안할 경우도 있어서 범위적으로 값을 넣어줘야하기에 더 어려운 일이라 생각하고, 역순으로 갔다.

- n= 7 -> 0, n번째 상담의 소요시간이 n일과 합했을때 퇴사일을 넘길 경우 dp[n] = dp[n+1]

- dp[i] = max(dp[i+1], pays[i] + dp[i+times[i]])

• dp[i+1] = 그날 상담을 진행하지 않는경우
• pays[i] + dp[i+times[i]] = 상담을 진행하는 경우

- dp의 최댓값 출력

import Foundation

let count = Int(String(readLine()!))!
var dp = Array(repeating: 0, count: count+1)
var pays = [Int]()
var times = [Int]()

for i in 0..<count {
    let inputs = readLine()!.split(separator: " ").map{Int(String($0))!}
    times.append(inputs[0])
    pays.append(inputs[1])
}

for i in stride(from: count-1, to: -1, by: -1) {
    if times[i] + i > count {
        dp[i] = dp[i+1]
    } else {
        dp[i] = max(dp[i+1], pays[i] + dp[i+times[i]])
    }
}
print(dp.max()!)

내가 푼 풀이

- 위 규칙 첫번째에 의하면 이친수는 무조건 1로 시작한다.

- 1이 연속으로 나타날 수 없다. 0은 연속으로 가능하다.

- N = 1 일때, 이진수는 0 , 1 ---> 이친수 : 1

- N = 2 일때, 이진수는 00, 01, 10, 11 ---> 이친수: 10

- N = 3 일때, 이진수는 000, 001, 010, 011, 100, 101, 110, 111 ---> 이친수: 100, 101

- 규칙에따라 첫번째 숫자가 무조건 1이여야하고, 1이 연속으로 나올 수 없다면, N이 3이상부터는 모든 이친수가 10으로 시작해야한다.

- N이 4 일때 10 _ _

• N = 3, 이친수의 뒤 두자리:  00 01
• N = 2, 이친수의 뒤 두자리: 10
• N = 4 일때의 이친수: 1010, 1000, 1001    //  3개

- N이 5일때 10 _ _ _

• N = 4, 이친수의 뒤 세자리: 010, 000, 001
• N = 3, 이친수의 뒤 세자리: 100, 101
• N= 5 일때의 이친수: 10100, 10101, 10010, 10000, 10001  //  5개

이를 점화식으로 나타내면 dp[n] = dp[n-1] + dp[n-2]   //  (dp[n] 은 n자리수의 이친수 갯수)

import Foundation

let count = Int(String(readLine()!))!
var dp = Array(repeating: 0, count: count+1)
dp[1] = 1

if count == 1 {
    print(dp[1])
} else {
    dp[2] = 1
    if count > 2 {
        for i in 3...count {
            dp[i] = dp[i-1] + dp[i-2]
        }
        print(dp[count])
    } else {
        print(dp[2])
    }
}

문제

재원이는 한 도시의 시장이 되었다. 이 도시에는 도시를 동쪽과 서쪽으로 나누는 큰 일직선 모양의 강이 흐르고 있다. 하지만 재원이는 다리가 없어서 시민들이 강을 건너는데 큰 불편을 겪고 있음을 알고 다리를 짓기로 결심하였다. 강 주변에서 다리를 짓기에 적합한 곳을 사이트라고 한다. 재원이는 강 주변을 면밀히 조사해 본 결과 강의 서쪽에는 N개의 사이트가 있고 동쪽에는 M개의 사이트가 있다는 것을 알았다. (N ≤ M)

재원이는 서쪽의 사이트와 동쪽의 사이트를 다리로 연결하려고 한다. (이때 한 사이트에는 최대 한 개의 다리만 연결될 수 있다.) 재원이는 다리를 최대한 많이 지으려고 하기 때문에 서쪽의 사이트 개수만큼 (N개) 다리를 지으려고 한다. 다리끼리는 서로 겹쳐질 수 없다고 할 때 다리를 지을 수 있는 경우의 수를 구하는 프로그램을 작성하라.

내가 푼 풀이

- 서쪽의 사이트보다 동쪽의 사이트가 같거나 많다.

- 같은 사이트에서 두개의 다리가 연결되거나, 다리끼리 x자로 교차로 설치되면 안된다. (중복 x)

- 중복되지않게 선택할 수 있는 경우의 수를 구하면 된다. ---> 조합

- 사이트 수가 적어서 직접 조합을 구해서 결과를 출력해도 좋지만, dp를 이용해서 풀어본다.

- dp[i][j] = iCj 이고 조합의 성질을 이용한다.

import Foundation

let count = Int(String(readLine()!))!
var dp = Array(repeating: Array(repeating: 0, count: 30), count: 30)
for i in 1..<30 {
    for j in 0...i {
        if j == 0 || i == j {
            dp[i][j] = 1
            continue
        }
            dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
    }
}

for i in 0..<count {
    let arr = readLine()!.split(separator: " ").map{ Int(String($0))! }
    print(dp[arr[1]][arr[0]])
}

사진출저:

내가 푼 풀이

- 길이 n의 계단 수를 구한다( 각 자리수의 차이가 1)

- i: 길이, j: 마지막자리의 숫자로 dp[i][j] 는 길이가 i인 마지막숫자 j가 오는 계단수의 갯수로 정의한다.

- dp[1][j] = 1 (  0 < j < 10 )

- 마지막자리 숫자가 0 인경우, 앞자리 수는 반드시 1 이와야하고, 마지막자리가 9라면, 앞자리 수는 반드시 8이어야 계단수가 성립한다.

- 나머지의 경우 는 마지막자리수 j의 앞자리수는 j-1 , j+1 이 될 수 있다.

- 이를 점화식으로 표현하면

• if j == 0 , dp[i][0] = dp[i-1][1]
• if j == 9 , dp[i][9] = dp[i-1][8]
• dp[i][j] = dp[i-1][j-1] + dp[i-1][j+1]

- dp값을 넣어줄때 항상 10억으로 나눠주고, 결과도 10억으로 나눠서 출력한다.

import Foundation

let num = Int(String(readLine()!))!
var dp = Array(repeating: Array(repeating: 0, count: 10), count: num+1)

for i in 1...9 {
    dp[1][i] = 1
}

if num == 1 {
    print(dp[num].reduce(0, +))
} else {
    for i in 2...num {
        for j in 0...9 {
            if j == 0 {
                dp[i][j] = dp[i-1][1] % 1000000000
            } else if j == 9 {
                dp[i][j] = dp[i-1][8] % 1000000000
            } else {
                dp[i][j] = (dp[i-1][j-1] + dp[i-1][j+1]) % 1000000000
            }
        }
    }
    
    print(dp[num].reduce(0, +) % 1000000000)
}

문제

2×n 직사각형을 1×2, 2×1과 2×2 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오.

아래 그림은 2×17 직사각형을 채운 한가지 예이다.

내가 푼 풀이

- n = 1 -> 1, n = 2 -> 3

- n = i 일때, 직사각형을 채울수 있는 방법은 3가지이다.

dp[i]는 2 x i 까지 채울수있는 직사각형의 경우의 수라고 한다면

1) i-1 까지 놓을 수 있는 경우의 수 + 2x1 타일을 놓는것 : dp[i-1]

2) i-2 까지 놓을 수 있는 경우의 수 + 2x2 타일을 놓는것 : dp[i-2]

3) i-2 까지 놓을 수 있는 경우의 수 + 2x2타일을 놓아 반으로 나눈 1x2타일 두개를 놓는것 : dp[i-2]

---> dp[i] = dp[i-1] + dp[i-2] + dp[i-2] 가 된다.

import Foundation

let count = Int(String(readLine()!))!
var dp = Array(repeating: 0, count: count+1)
dp[1] = 1

if count == 1 {
    print(dp[1])
} else {
    dp[2] = 3
    if count == 2 {
        print(dp[2])
    } else {
        for i in 3...count {
            dp[i] = (dp[i-1] + (2 * dp[i-2])) % 10007
        }
        print(dp[count])
    }
}

내가 푼 풀이

- 이 문제는 2579번 계단오르기 문제와 유사하다.

- 연속된 3개의 잔은 먹을수 없다.

- 계단오르기문제와 차이점은 계단은 n번째 계단을 올라가야 그 이후 계단을 오를수있지만, 포도주는 아예 안먹을 수 있다.

- 첫번째와 두번째 포도주까지는 무조건 먹는것이 포도주의양 최댓값이다.

- 1번째 포도주: dp[1] = arr[1], 2번째 포도주: dp[2] = arr[1] + arr[2]

- 세번째부터 i번째까지, i번째 포도주를 먹는경우: max(dp[i-2] + arr[i], dp[i-3] + arr[i-1] + arr[i])

- dp[i] 를 먹는경우로 저장하고 이제 먹지않는 경우를 비교한다. dp[i] = max(dp[i-1], dp[i])

- dp[i-1]와 dp[i] 를 비교한 이유는 dp[i-1]은 i-1번째 포도주를 마신경우의 최댓값이다.

- 여기서 i-1, i-2 를 연달아 마신경우, i-3 i-1로 마신경우 모두 포함하므로 dp[i-1] 과 비교하였다.

import Foundation

let count = Int(String(readLine()!))!
var dp = Array(repeating: 0, count: count+1)
var arr = [0]
dp[0] = 0
for i in 0..<count {
    arr.append(Int(String(readLine()!))!)
}

dp[1] = arr[1]
if count != 1 {
    dp[2] = arr[1] + arr[2]
    if count > 2 {
        for i in 3...count {
            dp[i] = max(dp[i-2] + arr[i], dp[i-3] + arr[i-1] + arr[i])
            dp[i] = max(dp[i-1], dp[i])
        }
    }
}
print(dp.max()!)

문제

오른쪽 그림과 같이 삼각형이 나선 모양으로 놓여져 있다. 첫 삼각형은 정삼각형으로 변의 길이는 1이다. 그 다음에는 다음과 같은 과정으로 정삼각형을 계속 추가한다. 나선에서 가장 긴 변의 길이를 k라 했을 때, 그 변에 길이가 k인 정삼각형을 추가한다.

파도반 수열 P(N)은 나선에 있는 정삼각형의 변의 길이이다. P(1)부터 P(10)까지 첫 10개 숫자는 1, 1, 1, 2, 2, 3, 4, 5, 7, 9이다.

N이 주어졌을 때, P(N)을 구하는 프로그램을 작성하시오.

내가 푼 풀이

- P(1) = 1, P(2) = 1, P(3) = 1, P(n) = P(n-2) + P(n-3) 임을 알수있다. (n > 3) 

- 해당 점화식을 넣어서 P(N)값 출력

import Foundation

let count = Int(String(readLine()!))!

for i in 0..<count {
    let num = Int(String(readLine()!))!
    var dp = Array(repeating: 0, count: num+1)
    
    if num <= 3 {
        dp[num] = 1
        print(dp[num])
    } else {
        for i in 1...num {
            if i <= 3 {
                dp[i] = 1
                continue
            }
            dp[i] = dp[i-2] + dp[i-3]
        }
        print(dp[num])
    }

}