문제 설명
A도둑과 B도둑이 팀을 이루어 모든 물건을 훔치려고 합니다. 단, 각 도둑이 물건을 훔칠 때 남기는 흔적이 누적되면 경찰에 붙잡히기 때문에, 두 도둑 중 누구도 경찰에 붙잡히지 않도록 흔적을 최소화해야 합니다.
물건을 훔칠 때 조건은 아래와 같습니다.
- 물건 i를 훔칠 때,
- A도둑이 훔치면 info[i][0]개의 A에 대한 흔적을 남깁니다.
- B도둑이 훔치면 info[i][1]개의 B에 대한 흔적을 남깁니다.
- 각 물건에 대해 A도둑과 B도둑이 남기는 흔적의 개수는 1 이상 3 이하입니다.
경찰에 붙잡히는 조건은 아래와 같습니다.
- A도둑은 자신이 남긴 흔적의 누적 개수가 n개 이상이면 경찰에 붙잡힙니다.
- B도둑은 자신이 남긴 흔적의 누적 개수가 m개 이상이면 경찰에 붙잡힙니다.
각 물건을 훔칠 때 생기는 흔적에 대한 정보를 담은 2차원 정수 배열 info, A도둑이 경찰에 붙잡히는 최소 흔적 개수를 나타내는 정수 n, B도둑이 경찰에 붙잡히는 최소 흔적 개수를 나타내는 정수 m이 매개변수로 주어집니다. 두 도둑 모두 경찰에 붙잡히지 않도록 모든 물건을 훔쳤을 때, A도둑이 남긴 흔적의 누적 개수의 최솟값을 return 하도록 solution 함수를 완성해 주세요. 만약 어떠한 방법으로도 두 도둑 모두 경찰에 붙잡히지 않게 할 수 없다면 -1을 return해 주세요.
제한사항
- 1 ≤ info의 길이 ≤ 40
- info[i]는 물건 i를 훔칠 때 생기는 흔적의 개수를 나타내며, [A에 대한 흔적 개수, B에 대한 흔적 개수]의 형태입니다.
- 1 ≤ 흔적 개수 ≤ 3
- 1 ≤ n ≤ 120
- 1 ≤ m ≤ 120
테스트 케이스 구성 안내
아래는 테스트 케이스 구성을 나타냅니다. 각 그룹 내의 테스트 케이스를 모두 통과하면 해당 그룹에 할당된 점수를 획득할 수 있습니다.
그룹총점테스트 케이스 그룹 설명
| #1 | 15% | info[i][1] = 1 |
| #2 | 40% | info의 길이 ≤ 20 |
| #3 | 45% | 추가 제한 사항 없음 |
입출력 예infonmresult
| [[1, 2], [2, 3], [2, 1]] | 4 | 4 | 2 |
| [[1, 2], [2, 3], [2, 1]] | 1 | 7 | 0 |
| [[3, 3], [3, 3]] | 7 | 1 | 6 |
| [[3, 3], [3, 3]] | 6 | 1 | -1 |
내가 푼 풀이
첫번째 방법 - DFS
한개의 물건이 주어졌을 때, 두가지 경우의 수가 있습니다.
1. A가 훔치기
2. B가 훔치기
또한 경찰에게 걸리지 않게 모든 물건을 훔쳤기에 물건을 훔치지 않는 옵션은 없습니다.
결국 A가 최소로 도둑질을 하면 흔적도 자연스럽게 최솟값을 가질 것이라 생각하고, B에게 먼저 조건을 걸어주었고, B가 최대한 훔치도록 구현하였습니다.
import Foundation
func solution(_ info:[[Int]], _ n:Int, _ m:Int) -> Int {
var min = Int.max
var informations = info
func dfs(count: [Int], currentIndex: Int) {
if currentIndex >= info.count {
min >= count[0] ? min = count[0] : nil
return
}
let theifACount = [count[0] + info[currentIndex][0], count[1]]
let theifBCount = [count[0], count[1] + info[currentIndex][1]]
if theifACount[0] < n && theifACount[0] < min {
dfs(count: [count[0] + info[currentIndex][0], count[1]],
currentIndex: currentIndex + 1)
}
if theifBCount[1] < m {
dfs(count: [count[0], count[1] + info[currentIndex][1]],
currentIndex: currentIndex + 1)
}
}
dfs(count: [0, 0], currentIndex: 0)
return min == Int.max ? -1 : min
}
결과는 시간초과가 발생하였습니다.
이유를 확인해보면, 만약 m,n이 매우 넉넉하다면, 큰 수라면 bfs의 실행은 $2^{40}$ 번 실행되어 시간초과가 발생하였습니다.
그러면 시간만 줄여서 될까 해서 테스트케이스를 몇 개 추가했더니, 해당 케이스도 실패하는걸 볼 수 있었습니다.
info = [[1, 2], [3, 1], [3, 2]]
n = 5
m = 3
// 결과는 4가 나와야 하지만 1이 나왔습니다.이를 통해 매번 탐색할 때 최적해를 갱신해야 할 필요가 있구나 싶었습니다.
두번째 방법 - DP
이전까지의 최적해를 저장하여 그다음 최적해를 구하기 위해 DP를 사용했습니다.
info배열을 돌면서 한번으로 최적해가 구해질 수 있을까? 해서 작성해보았는데 위 테스트 케이스도 통과하지 못했습니다.
B도둑이 알뜰살뜰하게 m을 넘지 않으면서 m과 가까운 수만큼 흔적을 남기는 방법이 뭐가 있을까 하다가 배낭문제가 생각났습니다.
(도둑이 배낭에 보석을 담을 때 정해진 배낭무게, 보석무게와 가치에 맞춰서 가장 가치있는 보석만 골라담는 문제)
B도둑이 최대한 흔적을 많이 남길 수 있게 배낭문제처럼 m값을 갱신하고 A흔적의 최솟값을 구하려고 합니다.
이를 1번 입력을 예시로 2차원배열로 나타내보겠습니다.

행은 m, B가 남길 수 있는 흔적 입니다. 열은 index로 info의 물건을 접근하기위한 인덱스입니다.
조건을 다시 살펴보자면,
1. 모든 물건을 훔쳤다.(물건을 훔치지 않고 건너뛰는건 불가능)
2. A는 n, B는 m 보다 같거나 클 수 없다. 만약 같거나 크다면 훔칠 수 없다고 판단한다.
위 조건을 바탕으로 배낭문제 처럼 2차원 배열을 채워가며 A의 최솟값을 구하겠습니다.
dp[i][j] = 0 은 물건을 하나도 훔치지 않을 때 값입니다.
행은 무게를 뜻하고, 열은 물건의 순서를 뜻하고, 해당 위치의 원소는 A의 흔적입니다.
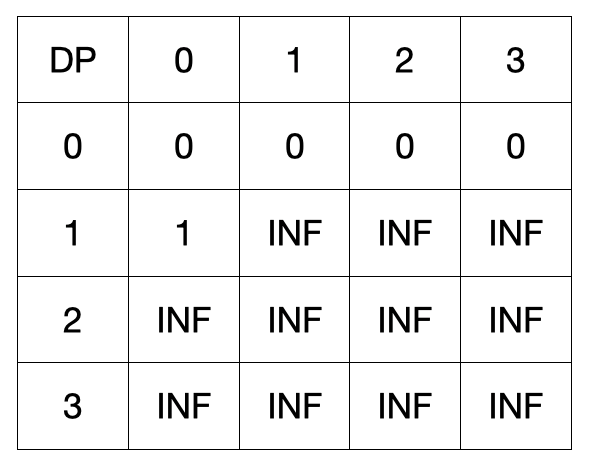
첫번째는 아무것도 훔치지 않았기때문에 dp[0][1...3] = 0 입니다.

이제 첫번째 물건을 훔치겠습니다. 물건의 정보는 [1, 2] 입니다.
이때, 두가지 경우의 수가 있습니다. (1. A가 훔치기 2. B가 훔치기)
해당 DP인덱스의 원소는 A의 흔적을 의미하기에 A가 훔친다면 이전 값에서 A의 흔적을 더한값이 될 것입니다.
B가 훔친다면, (현재열 + 2) 인덱스에 이전 값을 넣게 됩니다.
이렇게 이전의 저장된 값을 바탕으로 최적해를 구하기위해 갱신하면 다음과 같습니다.
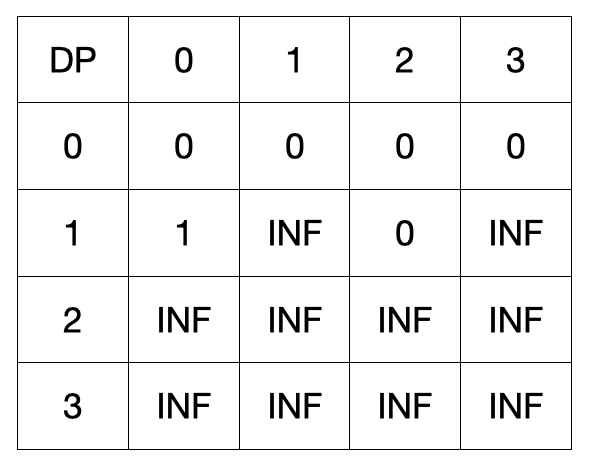
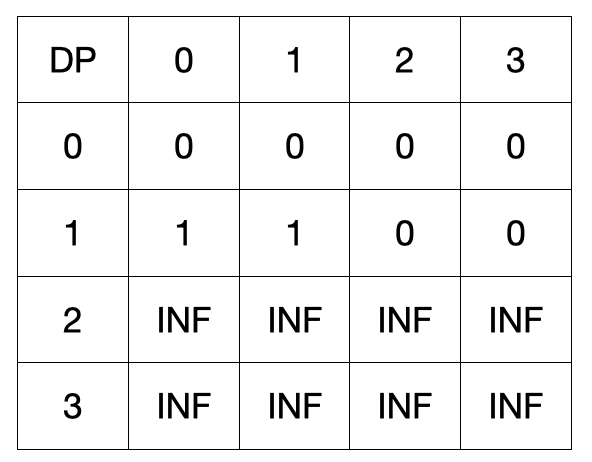
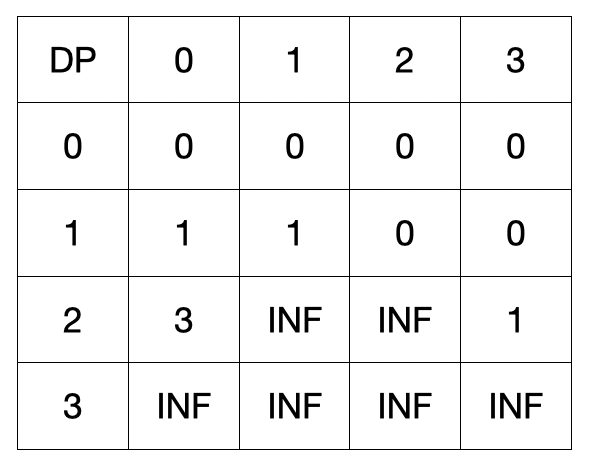
그 다음 두번째 물건을 훔치겠습니다. 물건의 정보는 [2,3] 입니다.
두번째 물건도 두가지 경우가 있습니다.
dp[2][0]에는 3이 들어가고 이 의미는 두번째 물건까지 A가 훔치는 경우입니다.
두번째 물건을 B가 훔치는 경우는 (현재 열 + 3) 인덱스에 넣게 되는데, 이 때 첫번째 물건을 넣은 값과 비교를 해야합니다.
dp[2][j + 3] = min ( dp[2][j + 3], dp[1][j] )
j = 0일때, dp[2][3] = min(dp[2][3], dp[1][0]) 을 비교하게 됩니다. (INF > 1)
이를 m = 3까지 갱신해줍니다.
dp[2][1], dp[2][2]는 첫번째는 B, 두번째는 A가 훔친경우입니다. 첫번째와 두번째 둘다 A가 훔친 경우(dp[2][0])보다 작은 수 이므로 갱신했습니다.
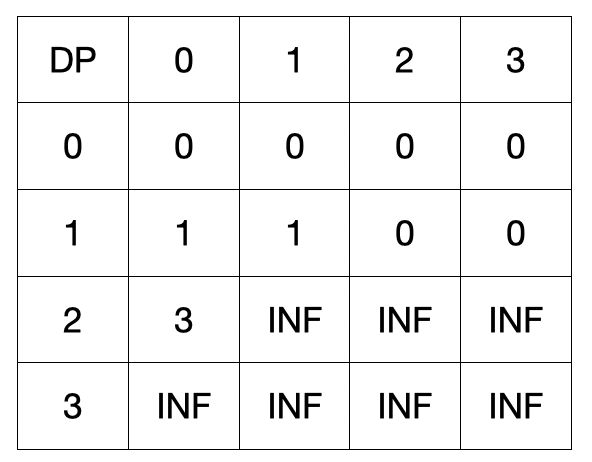
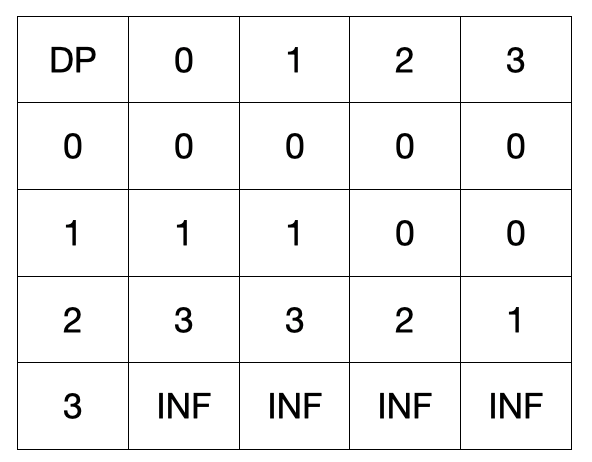
마지막으로 세번째 물건을 훔치겠습니다. 물건 정보는 [2,1]입니다.
세번째 물건까지 A가 훔치면 dp[3][0] = 5입니다.
세번째 물건을 B가 훔치는 경우라면 현재 인덱스 + 1의 자리를 갱신해줍니다.
dp[3][1] = min (dp[3][1], dp[2][1]) = 3
m = 3까지 갱신해주면 아래와 같습니다.
최종적으로 dp[3][3]에 구하는 값을 나타낼 수 있음을 알 수 있습니다.
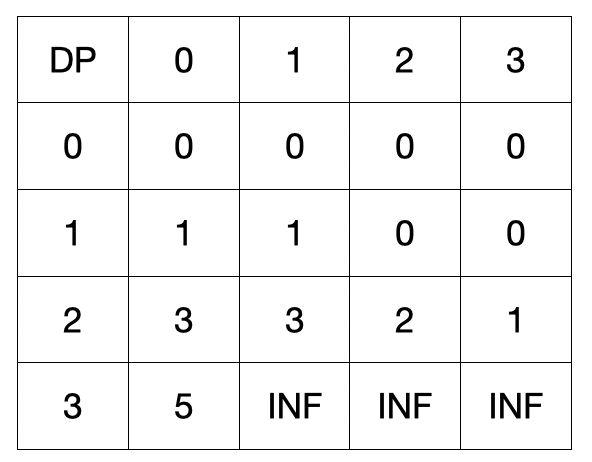
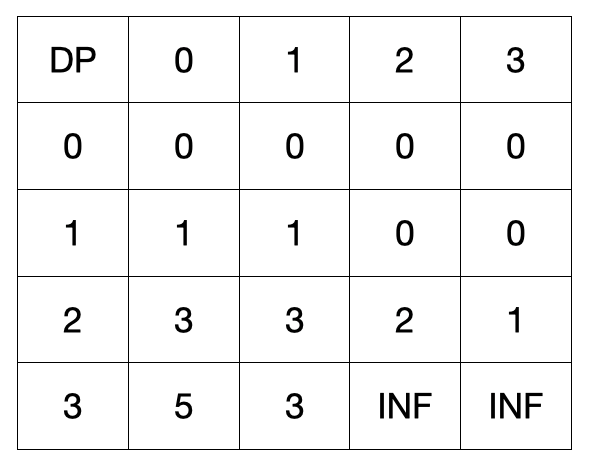
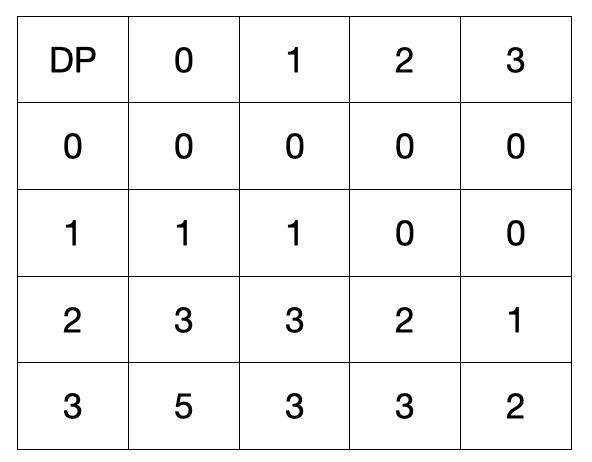
여기까지 살펴본 결과 2차원 배열의 의미를 다음과 같이 나타낼 수 있습니다.
dp[i][j]
- i : 현재 물건의 인덱스
- j : 현재 B의 흔적
- dp[i][j]의 원소: i번째 물건까지 훔쳤고 현재 B의 흔적이 j일때 A의 흔적 값
점화식은 아래와 같습니다.
- A가 훔쳤을 때 : dp[i][j] = min(dp[i][j], dp[i-1][j] + a) (a는 해당물건의 A흔적)
- B가 훔쳤을 때 : dp[i][j+b] = min(dp[i][j+b], dp[i-1][j]) (b는 해당물건의 B흔적)
코드로 나타내면 다음과 같습니다.
import Foundation
func solution(_ info:[[Int]], _ n:Int, _ m:Int) -> Int {
let INF = 100000000
// DP
var dp = Array(repeating: Array(repeating: INF, count: m),
count: info.count+1)
for i in 0..<m {
dp[0][i] = 0
}
for i in 1...info.count {
// 현재 물건에 대한 A의 흔적과 B의 흔적
let aThief = info[i-1][0]
let bThief = info[i-1][1]
for j in 0..<m {
// A가 훔친 경우 값 갱신
dp[i][j] = min(dp[i][j], dp[i-1][j] + aThief)
// B가 훔친 경우 값 갱신
if j + bThief < m {
dp[i][j + bThief] = min(dp[i][j + bThief], dp[i-1][j])
}
}
}
// 마지막 물건과 B의 흔적이 m보다 크거나 같지 않게 훔쳤을 때의 최소값 리턴
return dp[info.count][m-1] >= n ? -1 : dp[info.count][m-1]
}'코딩테스트 > 프로그래머스' 카테고리의 다른 글
| [프로그래머스] 서버 증설 횟수 Swift (0) | 2025.03.27 |
|---|---|
| [프로그래머스] 가장 먼 노드 Swift (0) | 2025.03.26 |
| [프로그래머스] 미로 탈출 Swift (1) | 2024.04.23 |
| [프로그래머스] 행렬 테두리 회전하기 Swift (0) | 2024.04.23 |
| [프로그래머스] 수식 최대화 Swift (0) | 2024.04.22 |
