문제
어떤 극장의 좌석은 한 줄로 되어 있으며 왼쪽부터 차례대로 1번부터 N번까지 번호가 매겨져 있다. 공연을 보러 온 사람들은 자기의 입장권에 표시되어 있는 좌석에 앉아야 한다. 예를 들어서, 입장권에 5번이 쓰여 있으면 5번 좌석에 앉아야 한다. 단, 자기의 바로 왼쪽 좌석 또는 바로 오른쪽 좌석으로는 자리를 옮길 수 있다. 예를 들어서, 7번 입장권을 가진 사람은 7번 좌석은 물론이고, 6번 좌석이나 8번 좌석에도 앉을 수 있다. 그러나 5번 좌석이나 9번 좌석에는 앉을 수 없다.
그런데 이 극장에는 “VIP 회원”들이 있다. 이 사람들은 반드시 자기 좌석에만 앉아야 하며 옆 좌석으로 자리를 옮길 수 없다.
오늘 공연은 입장권이 매진되어 1번 좌석부터 N번 좌석까지 모든 좌석이 다 팔렸다. VIP 회원들의 좌석 번호들이 주어졌을 때, 사람들이 좌석에 앉는 서로 다른 방법의 가짓수를 구하는 프로그램을 작성하시오.
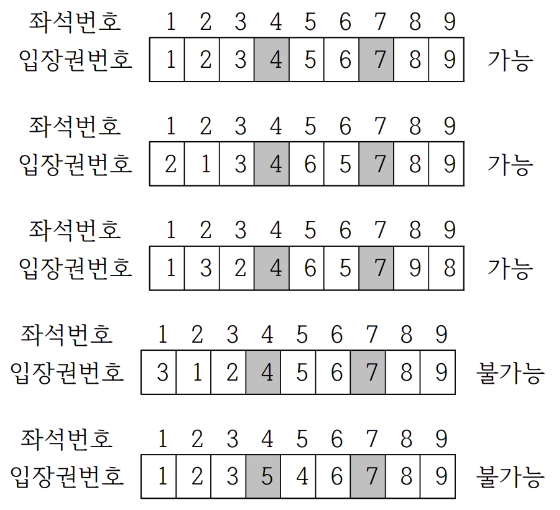
예를 들어서, 그림과 같이 좌석이 9개이고, 4번 좌석과 7번 좌석이 VIP석인 경우에 <123456789>는 물론 가능한 배치이다. 또한 <213465789> 와 <132465798> 도 가능한 배치이다. 그러나 <312456789> 와 <123546789> 는 허용되지 않는 배치 방법이다.
입력
첫째 줄에는 좌석의 개수 N이 입력된다. N은 1 이상 40 이하이다. 둘째 줄에는 고정석의 개수 M이 입력된다. M은 0 이상 N 이하이다. 다음 M 개의 줄에는 고정석의 번호가 작은 수부터 큰 수의 순서로 한 줄에 하나씩 입력된다.
출력
주어진 조건을 만족하면서 사람들이 좌석에 앉을 수 있는 방법의 가짓수를 출력한다. 방법의 가짓수는 2,000,000,000을 넘지 않는다. (2,000,000,000 < $2^{31}$-1)
내가 푼 풀이
접근방법: DP
각 좌석은 양 옆으로만 배치할 수 있다.
예시로 [1, 2, 3, 4] 좌석을 배치하는 경우의 수를 확인해보자.
[1]: [1] 1가지
[1, 2]: [1, 2], [2, 1] 2가지
[1, 2, 3]: [1, 2, 3], [2, 1, 3], [1, 3, 2] 3가지
[1, 2, 3, 4]: [1, 2, 3, 4], [2, 1, 3, 4], [1, 3, 2, 4], [1, 2, 4, 3], [2, 1, 4, 3] 5가지
위 좌석 4개로 규칙을 알 수 있다.
3개의 좌석 배치수를 구할 때: (2개 좌석이 배치된경우) + (3의 위치를 바꾼 경우)
( [1,2] + [3] , [2,1] + [3] ) + ( [1] + [3, 2] ) 으로 총 3가지
4개의 좌석 배치수를 구할 때: (3개의 좌석이 배치된 경우) + (4의 위치를 바꾸는 경우)
( [1,2,3] + [4] , [2,1,3] + [4] , [1,3,2] + [4]) + ( [1,2] + [4,3] , [2,1] + [4,3] )으로 총 5가지
이를 점화식으로 나타내면 다음과 같다.
dp[n] = dp[n-1] + dp[n-2]
여기서 추가조건으로 vip석은 이동할 수 없다.
위 예제를 보면 vip를 제외한 좌석은 아래와 같다.
[1,2,3] , [5,6] , [8,9]
각각 배치가능한 경우의 수를 구하면, 3 , 2 , 2 가 되고, 모두 곱하면 12가 나온다.
이렇게 vip좌석을 경계로 배치방법 수를 구하고 모두 곱해주면 결과가 나오게 된다.
코드에서는 중간 결과값을 저장하여 마지막 수와 곱해서 출력했다.
import Foundation
//입력받기
let N = Int(readLine()!)!
let M = Int(readLine()!)!
var vip = [Int]()
for i in 0..<M {
vip.append(Int(readLine()!)!)
}
// dp[n]: 중간 vip좌석 없이 n번째까지의 배치 경우의 수
var dp = Array(repeating: 1, count: N+1)
// vip좌석을 만나면 값을 저장할 변수
var mul = 1
var idx = 0
var vp = false
// 탐색
for i in 1...N {
// vip좌석을 만나면 중간값 저장
if idx < M && i == vip[idx] {
idx += 1
dp[i] = 1
mul = dp[i-1] * mul
vp = true
continue
}
// 이전에 vip좌석이였다면 그 다음 배치경우의수는 좌석 1개이므로 1
if vp {
dp[i] = 1
vp = false
continue
}
// 첫번째 좌석은 경우의수가 1가지
if i == 1 {
dp[i] = 1
continue
}
dp[i] = dp[i-1] + dp[i-2]
}
print(dp[N] * mul)
//print(mul)
'코딩테스트 > 백준' 카테고리의 다른 글
| BOJ-7579 앱 Swift (0) | 2024.05.30 |
|---|---|
| BOJ-2011 암호코드 Swift (0) | 2024.05.19 |
| BOJ-1937 욕심쟁이 판다 Swift (0) | 2024.05.14 |
| BOJ-11049 행렬 곱셈 순서 Swift (0) | 2024.05.13 |
| BOJ-25682 체스판 다시 칠하기 2 Swift (0) | 2024.05.11 |

